Blog
Gerrymandering is the reason that some countries (I’m looking at you, United States) end up with weird electoral districts that look like this one from Illinois:
Or this one from Arizona:
Politicians stretch and distort their districts to these weird shapes for two reasons:
To get more seats for themselves.
To get re-elected without having to run any kind of real campaign.
It’s one of the reasons that, in the United States, the re-election rates for the House of Representatives has been over 85% in every cycle since 1964.
While looking in to solutions for this problem, I came across the interesting people at rangevoting.org who have an solution called ‘shortest split-line’ explained below:
To see some real-world results from their method, here are the current districts for my home state of New York:
And here is how they would look with the split-line method:
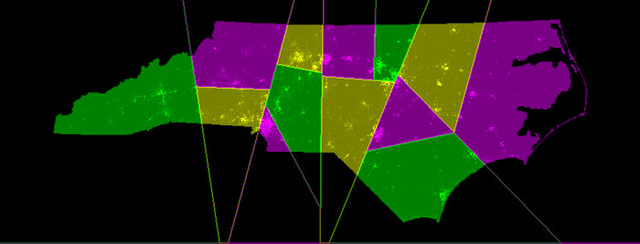
North Carolina, where my parents live, have these districts:
Which are much improved with the split-line method:
And, not that it would ever happen, but if you ignored state lines, all the districts in the House of Representatives would look like this:
While shortest split-line districting would solve the wacky (and unfair) shapes of modern districts, it still doesn’t do anything to help with the problem of two-party control:
Oh, and to cut the pedants off before they start, yes, I know that Gerrymandering is supposed to be pronounced with a hard ‘G’ like ‘Gary Busey’, but I’ve never heard an actual human in real life pronounce it like that, so I’m not going to either.
Script
Queen Lion of the Animal Kingdom is giving more democracy to her citizens by adding a legislative branch to the government.
The citizens each get one vote and are divided into ranges. Each range will elect one representative to send to the newly created Jungle Council.
To best understand how this system works, lets look at a small colony where there are just two political parties: Buffalo & Jackalope.
This colony is divided into four ranges. In the first election Jackalope candidates win two of them and buffalo candidates win the rest.
All is well for several election cycles until the Animal Kingdom Census taker comes round and shows that the population has both moved and grown.
To better represent the larger population a new seat is added to the Jungle council so the ranges’ boundaries must be re-drawn.
This is where the trouble begins. Re-drawing electoral boundaries is a huge political problem.
To help them, the representatives of the Jungle Council hire a weaselly consultant to figure out where the new boundaries should go.
If Weasel draws rectangular boundaries everything is OK because the jungle council will, as close as possible, reflect how the citizens vote.
However, Weasel doesn’t do this. Instead he tells the Buffalo Party that, for a price, he can turn their slim majority into a landslide victory in the election.
With a super-majority on the Jungle Council the Buffalo wouldn’t have to listen to those pesky Jackalope filibusters anymore, so the Buffalo gladly pay up.
How can Weasel deliver on his promise? It’s depressingly simple: by packing together as many jackalope voters into one range as possible and spreading the rest of them out, The Buffalo Party can win an additional seat without any voters switching allegiance.
What Weasel and the Buffalo have done is called ‘gerrymandering’. The intensional changing of electoral boundaries for their benefit.
Several election cycles later the under-represented and disgruntled Jackalope party approaches Weasel and asks if he can manipulate the ranges to be in their favor instead of the Buffalos’.
Indeed he can. Using the same trick, Weasel packs Buffalo voters into a few ranges and spreads the rest among the Jackalope supporters.
After the election the Jackalopes, who represent a minority of the voters are now, nonetheless, the majority party on the Jungle Council.
This is the terrible power of Gerrymandering: Weasel can take the exact same voters and get either party to win the election.
Unsurprisingly, Weasel’s business grows and eventually every colony in the Animal Kingdom pays him to gerrymander their ranges.
With so many clients, Weasel now uses his computer test hundreds of thousands of range combinations with elaborate statistical models of voter behavior to get the results he needs.
Queen Lion has seen what Weasel is up to and banishes him from her kingdom. But, the census taker reminds her that ranges still need to be re-drawn as the population changes. So how is it going to be decided?
Queen Lion suggests the obvious solution: a bi-partisan committee must agree on all new range boundaries.
This seems like a good idea. After all, if both parties have to agree on the ranges, then they must end up being fair to everyone.
But, after a few election cycles using this solution, Queen Lion notices that she always sees the same faces on the Jungle Council. Representatives almost never get defeated in their elections.
It turns out that the interests of the representatives and the interests of the citizens are not the same. Citizens want elections where the candidates have to earn their vote. These are close elections where either candidate has a chance of winning.
But, representatives don’t want close elections, they want safe elections. Elections where they run in a range that is filled with supporters.
Because the representatives are in change of the boundaries they make the safest ranges possible.
So, bi-partisan committees are not enough. To truly fix gerrymandering there are three options:
The first is to set up a politically independent commission of appointed experts or judges to draw the boundaries.
Independent commissions are much better than bi-partisan committees, but still not ideal because they usually group similar areas together so the elections are uncompetitive.
And there is always the possibility that the independent commission is not as independent as it appears.
The second option is to let math decide the boundaries. There are a number of ways to mathematically divide an area into equally populous ranges.
The simplest example of this is called the ‘shortest split-line method’. Find the shortest line that splits the voters in twain and repeat as necessary until all the ranges are made.
This is much better than an ‘independent’ commission, but it does have the problem of occasionally producing skewed election results just through pure bad luck of where the boundaries are drawn.
But by publishing the algorithm used, all citizens can check the results and be confident that there is no intensional bias in the system.
The last solution is an unexpected one: hire back the weasel and embrace gerrymandering. But this time, pay him make the winners most closely match the voters as a whole.
While it seems unsavory, this is actually the best way to avoid disproportionate representation which is, by far, the the worst problem of gerrymandering.
But, considering these three solutions leaves Queen Lion grumpy.
The first two are improvements, but still may result in uncompetitive elections or disproportionate results while the third just feels wrong. Gerrymandering to avoid the problems of gerrymandering is… odd.
Remembering what she learned about voting before, she realizes all this gerrymandering is really just a symptom of a more fundamental problem: the method by which each citizen gets only one vote and elects only one representative.
There are ways to eliminate gerrymandering and restore competitive elections to make her citizens happy, but to do that Queen Lion is going to have to make some big, fundamental changes to her democracy.
Credits:
Images by: Rictor Norton, David C Walker 1967, Billy Lindblom, xlibber, Todd Ryburn, shirobane, Dawn Huczek, TheBusyBrain, Stig Nygaard, Michael Baird, Ana_Cotta, digitalART2, be_khe, Hamed Saber, Pixel Addict, Shawn Allen, Aunt Owwee, Jack Dykinga (USDA), Mykl Roventine, Steve Jurvetson, Boss Tweed, Cecil Sanders, One Laptop Per Child, Martin Pettitt(2), Jim Bowen(2)(3), Brian Sneison, monkeywing, Andrea Allen & audreyjm529.